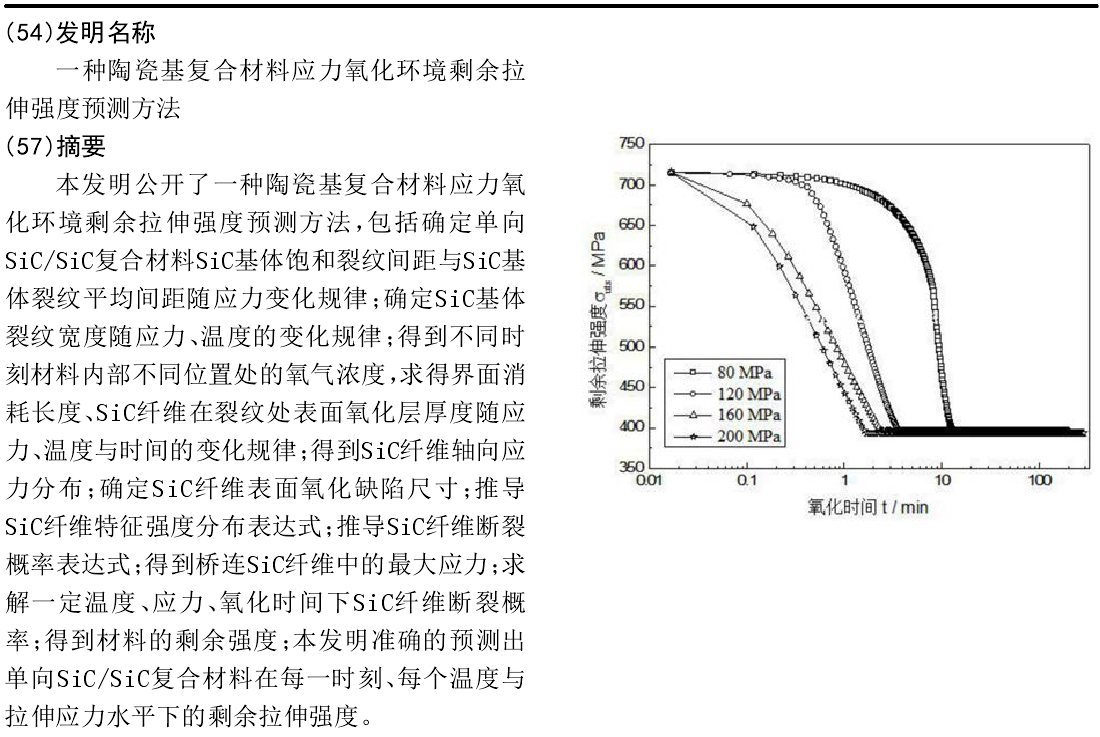
一种陶瓷基复合材料应力氧化环境剩余拉伸强度预测方法

1.一种陶瓷基复合材料应力氧化环境剩余拉伸强度预测方法,其特征在于,包括以下步骤：(1)、确定单向SiC/SiC复合材料SiC基体饱和裂纹间距与SiC基体裂纹平均间距随应力变化规律；(2)、确定SiC基体裂纹宽度随应力、温度的变化规律；(3)、建立单向SiC/SiC复合材料应力氧化动力学方程与边界条件,采用经典四阶龙格库塔法求解该方程,得到不同时刻材料内部不同位置处的氧气浓度,基于该氧气浓度值求得界面消耗长度、SiC纤维在裂纹处表面氧化层厚度随应力、温度与时间的变化规律；所述步骤(3)中,由于拉伸应力σ的作用,SiC基体表面会出现裂纹,假设裂纹沿垂直于SiC纤维方向,即y方向扩展,且均为贯穿裂纹,氧气从SiC基体裂纹处进入到界面处,将界面氧化,并沿着平行于SiC纤维方向,即z方向扩散；因此将氧气在材料内部的扩散分为SiC基体裂纹扩散阶段与界面层扩散阶段；所述步骤(3)中,所述SiC基体裂纹扩散阶段的氧化动力学方程为：  式中,Rt为SiC基体表面到SiC纤维圆心的距离,y表示SiC基体裂纹深度坐标值,hm(y,t)为在某一时刻t、某一SiC基体裂纹深度y处SiO2层相对于壁面突出的厚度,d为裂纹宽度e的1/2,C0为环境中的氧气浓度,为某一时刻t、某一SiC基体裂纹深度y处的氧气浓度,α为碳界面的氧化产物CO/CO2与氧气O2之间的摩尔通量的比值,表示氧气浓度在某一SiC基体裂纹深度y处的浓度梯度,gm表示SiC基体氧化生成1mol二氧化硅SiO2消耗的氧气摩尔数,ρs表示SiO2的密度,Bm表示SiC基体的抛物线速率常数,C*为一个标准大气压下纯氧环境下的氧气浓度,pm为SiC基体的氧气浓度指数,Ms为SiO2的摩尔质量,ym(t)为在t时刻SiC基体裂纹内部SiC基体表面SiO2层的厚度,其表示为：  D1为氧气的有效扩散系数,D1表示为：  式中,DAB为二元扩散系数,DKA为Knudsen扩散系数,其中：DAB表示为：  式中,T为环境温度,P为环境压强,(Σv)A和(Σv)B分别表示O2和CO/CO2分子的扩散体积,为混合气体的摩尔质量,表示为：  式中,MA和MB分别表示O2和CO/CO2分子的摩尔质量；DKA表示为：  式中,r为缺陷的特征半径,Rg为气体常数,π为圆周率；所述步骤(3)中,所述界面层扩展阶段的氧化动力学方程为：  式中,表示氧气在界面通道内沿着平行于SiC纤维的方向,即z方向的浓度梯度,Rm、Rf分别表示SiC纤维中心到SiC基体表面氧化层外表面的距离与SiC纤维中心到SiC纤维表面氧化层外表面的距离,D2与D1表达式相同,表示氧气在界面处的有效扩散系数,Bf表示SiC纤维的抛物线速率常数,pf为SiC纤维的氧气浓度指数,gm、gf分别表示SiC基体和SiC纤维中生成1mol SiO2所需要消耗的氧气的物质的量,yf(t)为t时刻SiC纤维表面SiO2氧化层的厚度,其通过下式求得：  所述步骤(3)中,边界条件分为三个部分,第一部分：在SiC基体裂纹顶端y＝0处的氧气浓度等于环境中的氧气浓度C0,即：  第二部分,在界面氧化处z＝lr,扩散到该处的O2的摩尔通量与界面消耗的O2的速率相等,即：  其中,pc表示碳氧化反应级数,k表示碳氧化速率常数,k表示为：  式中,γ表示预氧化因子,Er表示反应活化能；lr表示碳界面的消耗长度,lr通过下式求得：  式中,b为1mol氧气消耗的碳的物质的量,Mc和ρc分别为碳的摩尔质量和密度；第三部分,裂纹底部y＝L,z＝0,假设在该处氧气没有多余的消耗,其物质的量不发生变化,即：  式中,hm(t)表示某一时刻t下SiC基体裂纹底端y＝L处SiO2层相对于壁面突出的厚度；所述步骤(3)中,基于上述边界条件,采用经典四阶龙格库塔积分法分别求解上述SiC基体裂纹扩散阶段与界面层扩展阶段的氧化动力学方程,得到在不同时刻材料在SiC基体裂纹内部、界面通道处的氧气浓度值将该浓度值带入公式(8)中求得不同拉伸应力水平σ、温度T、时刻t下,基体裂纹处和界面通道裂纹处基体表面的氧化层厚度ym,将该浓度值带入公式(14)中求得不同拉伸应力水平σ、温度T、时刻t下,SiC纤维表面不同位置z处的氧化层厚度yf；将该浓度值带入公式(18)中求得不同拉伸应力水平σ、温度T、时刻t下,碳界面的消耗长度lr；(4)、根据界面消耗长度、SiC基体裂纹平均间距、SiC基体饱和裂纹间距与SiC基体裂纹宽度三者之间的大小关系,得到SiC纤维轴向应力分布；(5)、基于SiC纤维表面氧化层厚度,确定SiC纤维表面氧化缺陷尺寸；(6)、基于SiC纤维表面氧化缺陷尺寸与SiC纤维临界裂纹尺寸之间的大小关系,推导SiC纤维特征强度分布表达式；(7)、基于SiC纤维初始强度分布服从双参数威布尔分布的假设,推导SiC纤维断裂概率表达式；(8)、将SiC纤维断裂概率表达式带入单根SiC纤维在裂纹平面处的力的平衡方程,求解该方程得到桥连SiC纤维中的最大应力；(9)、将桥连SiC纤维中的最大应力代入SiC纤维断裂概率表达式,求解一定温度、应力、氧化时间下SiC纤维断裂概率；(10)、基于平均裂纹间距、界面消耗长度、裂纹宽度与SiC基体饱和裂纹间距之间的关系,判断采用多重开裂剩余强度模型或单裂纹开裂剩余强度模型计算得到材料的剩余强度。