基于电阻抗成像损伤监测的复合材料强度预测方法

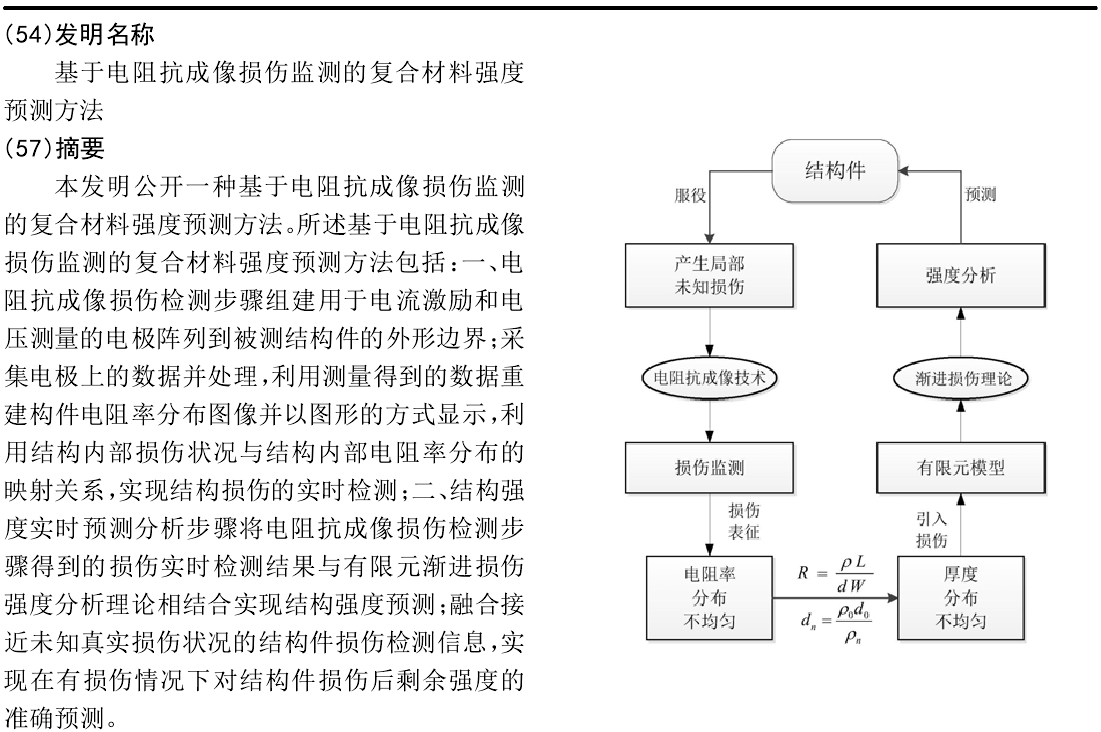
1.一种基于电阻抗成像损伤监测的复合材料强度预测方法,其特征在于,包括：一、电阻抗成像损伤检测步骤组建用于电流激励和电压测量的电极阵列到被测结构件的外形边界；采集电极上的数据并处理,利用测量得到的数据重建结构件电阻率分布图像并以图形的方式显示,利用结构内部损伤状况与结构内部电阻率分布的映射关系,实现结构损伤的实时检测；步骤一具体包括如下步骤：步骤1.1：制作电极,围绕被测结构件的四周组建用于连接电流激励和电压测量设备的电极阵列；步骤1.2：采集数据并处理,对被测结构件沿着边界电极施加多组激励,在施加一组激励的同时沿着边界测量得到多组边界电压；步骤1.3：利用EIT重构被测结构件电阻率,并显示分布图像；具体包括如下内容：EIT正问题是已知电导率σ求解被测结构件场域的电位分布φ,满足偏微分方程(1)及边界条件方程(2),且采用数值近似方法求解：▽·[σ(x,y)▽φ(x,y)]＝0,(x,y)∈Ω (1)  假设电极数为正整数N,将场域剖分成M个三角形单元,共K个结点,M、K均为正整数；用ρn,n＝1,2,…,M表示第n个单元的电阻率值,用Yi,i＝1,2,…,N表示在第i组激励电流下的总体刚度矩阵,用φim,i＝1,2,…,N；m＝1,2,…,K表示在第i组激励电流下场域中第m个结点处的电位；用Vij(ρ),i,j＝1,2,…,N表示在某一计算得到的电阻率ρ分布下,第i组激励下第j组计算得到的相邻电极上的边界电压数据；其中,Vij(ρ)＝T·φim,T为转换矩阵；EIT逆问题是已知电位分布φ求解被测结构件场域的电导率σ；对于被测结构件实际电阻率ρ*分布,用Uij,i,j＝1,2,…,N表示在第i组激励电流下第j组实验测量得到的相邻电极上的边界电压数据；EIT逆问题也就是根据该测量数据Uij来计算场域内电阻率ρ*的分布,电阻率ρ与电导率σ存在关系：ρ＝1/σ；在实际求解中,EIT逆问题就是数学上的最小二乘问题,寻求电阻率ρ分布,使得式(3)中的E(ρ)最小；  采用基于NOSER算法的改进算法实现EIT逆问题的求解,具体计算过程如下：1)利用有限元求解电阻率均匀为1条件下,场域相邻电极上的边界电压其中2)根据公式(4)计算初始电阻率  3)根据公式(5)计算  4)根据公式(5)-(8)计算雅克比矩阵J,雅克比矩阵J的逆J-1；  Bn,m＝γAn,mδn,m (7)Jn,m＝An,m+Bn,m (8)其中,γ为一很小的正实数,δ为一单位矩阵；5)根据公式(9)计算场域电阻率分布；ρ＝ρ(0)-[J(ρ(0))]-1·F(ρ(0)) (9)结果图像显示；假设每幅图片的像素尺寸为长L像素、宽W像素,其中L、W为正整数；每个像素具有RGB三种通道的颜色值,建立像素的颜色数组Color[R,G,B]；每个单元中各像素点的Color[R,G,B]相同,具有最大电阻率值ρmax的单元对应红颜色数组Color[255,0,0],具有最小电阻率值ρmin的单元对应蓝颜色数组Color[0,0,255],其余单元的颜色数组采用线性插值函数来计算；步骤1.4：实现损伤检测,利用具有导电性的材料在受损时,其电阻率会相应发生变化这一自检特性实现；在未产生局部损伤时,结构件上的电阻率分布近似均匀；在产生损伤后,局部损伤处由于内部微观构造发生改变,内部导电通路变化,造成该区域电阻率值突变；二、结构强度实时预测分析步骤将电阻抗成像损伤检测步骤得到的损伤实时检测结果与有限元渐进损伤强度分析理论相结合实现结构强度预测；融合接近未知真实损伤状况的结构件损伤检测信息,实现在有损伤情况下对结构件损伤后剩余强度的准确预测；步骤二具体包括如下步骤：步骤2.1：量化并引入损伤信息；电阻率是表示物质电阻特性的物理量,假设材料长L,宽W,厚d,S为横截面积,在温度一定的情况下,有公式(10)  考虑由EIT重建获得的第n个单元的电阻率ρn,由EIT技术的原理可知,在损伤产生前后,只有电阻率产生了变化；各单元厚度即构件厚度一致均设为d0,各单元电阻率在损伤前一致均设为ρ0；在电学模型中,有式(11)  假设dn为力学模型中第n个单元的厚度,因为后续的强度分析与电学分析所采用的有限元模型相同,所以该单元在电学模型中电阻率为ρn；力学模型中没有电阻率这一物理量,因此,将单元的电阻率变化等效为单元的厚度变化,有式(12)  联立式(11)、(12)即可获得力学分析中某一单元的电阻率ρn与厚度dn之间的转换关系式(13),从而实现了强度分析中损伤信息的量化和引入：  步骤2.2：预测强度；采用有限元渐进损伤强度分析理论预测结构件在实时检测到的损伤状况下的强度；采用位移加载的方式,在构件的一端施加固定约束,另一端施加位移载荷,所用复合材料的应力-应变响应关系由该材料的单轴拉伸试验数据拟合得到,失效准则采用最大应变准则,所用极限应变同样由试验获得；强度计算的理论依据包括用户自定义的材料刚度折减模型,模型的建立和求解基于有限元法实现。